前篇写的线性拟合，这种纯线性的方式很简单，但是实际应用中这种直上直下的场景还是很少。有复杂的情况怎么办呢？

来复习一个东西。一元N次多项式。

y=a+b*x+c*x^2+d*x^3+....+n*x^n

我们之前的线性拟合就是它的一个特例,一元一次多项式

y=a+b*x

那有没有办法,用N次多项式来拟合复杂的数据呢，答案是可以的。

我们先来搞出一个复杂一点的数据集。比如类正弦曲线。

library(ggplot2)set.seed(1)x1 = seq(0,1,by=0.01)y1 = sin(2*pi*x1) + rnorm(length(x1),0,0.1)df = data.frame(x=x1,y=y1)ggplot(df,aes(x=x1,y=y1))+geom_point()

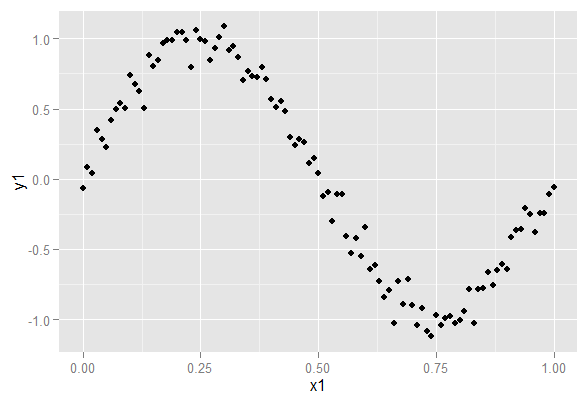
那么用纯线性拟合能出个什么结果呢？

很明显，这结果差的多。

现在我们多加几项数据来共同进行预测，加的数据就是x的n次方。

df = transform(df,x2 = x1^2)df = transform(df,x3 = x1^3)df = transform(df,x4 = x1^4)df = transform(df,x5 = x1^5)l = lm(y1~x1+x2+x3+x4+x5,data=df)df = transform(df,PreY = predict(l))ggplot(df,aes(x=x1,y=PreY))+geom_point()+geom_line()

前面的几个transform是给df数据集加上几列新的数据，为x1的2345次方。

lm用x1 x2 x3 x4 x5对y1进行求线性拟合，其实就是找最合适的各项系数。

下面再用predict的预测结果加到数据集中。

把预测结果可视化。

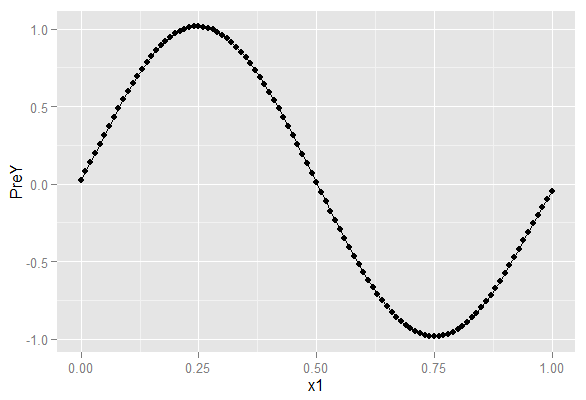
这个准多了是吧。

看到效果， 我们再来说一个新的函数poly，它的作用就是为简便的实现前面的工作。代替那一坨transform。看用法：

l = lm(y~poly(x,degree=5),data=df)

是不是简单的多，这degree的5就是前面我们生成的n次方的最大值。

那么新问题来了。

是不是这个degree的值越大。预测的越准呢？

让我们来继续看例子：

我们用25次方来拟合之前的数据集。

l = lm(y~poly(x,degree=25),data=df)df = transform(df,PreY = predict(l))ggplot(df,aes(x=x1,y=PreY))+geom_point()+geom_line()

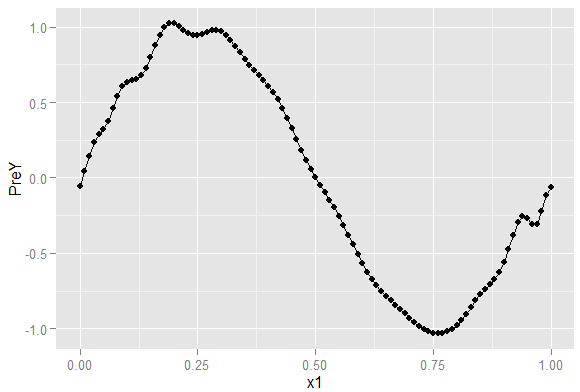
怎么变成这个熊样了。让我们来对比最初的数据图像和用5次多项式拟合的结果。

图是PreY1是用5次多项式拟合的，很标准的正弦线。PreY2是用25次多项式拟合的，就不怎么标准了。但是仔细观察就能发现，它更好的符合了y真实而细小的变化趋势。

嗯 。

结果好像还不错。

让我们来分析一下。在最初创建数据集的时候，我们引入了一些随机性。

这些随机性在应用中称为噪声。

在拟合的复杂度不是很高的时候，5次多项式，噪声被过滤了。

在高复杂度时，25次多项式，预测有能力尽可能的去贴合数据的变化，噪声被引入到预测结果中。这称为过拟合。

但是，在实际应用中，怎么能区别噪声和真实的变化呢？何以为”过“？

这个是问题。